Pemmaus
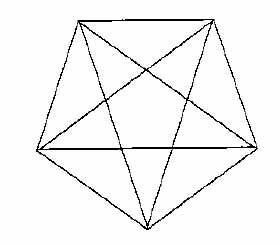
Wer kann helfen: Wie viel Dreiecke sind in dieser Figur enthalten?
Würde dir gern helfen aber welche figur den Smile etwar LOL ;)
Ups... sollte eigentlich mit Bild
Auf was kommt Ihr denn so? melli
elf?
mein Mann lol ich bin nur bis 18 gekommen da brauch mehr nerven
...
13? LG
.
Voll lustig..... 
ich mag solche Aufgaben...
melli
...
Hier findest du die Lösung:
http://www.mathematische-basteleien.de/zaehl_figuren.htm
27
barnie
...
LG
habe ich raus. Meine Tochter 15
erst alle einzelnen, also 11 dann alle aus 2 Teilen ich glaube 10 dann aus 3 Teilen 8 aus 5 teilen 4 zu mehr fehlt mir gerade die Zeit----ich müsste es dann auch ausdrucken und kanndas nciht *g*
aber guter Tipp Henni, Danke dafür. melli
s
Ich finde kein einziges Dreieck mit 4 Teilen! Ich finde 10 1er, 6 2er, 5 3er und 5 5er. *blindbin*
Fast, Henni einzeln 10 aus zwei Teilen 10 aus drei Teilen 8 aus 5 Teilen 3 macht auch 33 ;-)))
habe leider keine Zeit zu gucken, ob da noch mehr sind
LG
Stellst du bitte die richtige Lösung hier rein, wenn du sie hast? Aufgeteilt in die einzelnen Dreiecke aus jeweils wievielen Teilen? Büddebüdde!
Ja, mache ich... dauert aber ca. 14 Tage. Mein aktueller Stand ist: 1-Teil = 10 2-Teile = 7 3Teile = 7 5 Teile = 5 Macht 29. Aber ich muss auch noch mal den Farbstift zur Hand nehmen... das wird ja soooo unübersichtlich. LG Pem
Hallo, ich komme auf 35. LG Inge
Hallo, ohne doppelte, ich hab die Dreiecke mit Farbe nachgemalt. Nachdem die Figur auf einem gleichseitigen Fünfeck basiert und punktsymmetisch ist, muss auf jeden Fall das Ergebnis durch 5 Teilbar sein. Denn jedes "neue" Dreieck wiederholt sich ja auf jeder Seite wieder. LG Inge
owt.
...
10 x 1 10 x 2 8 x 3 5 x5 LG Sibs
Vlg, Anna
Ich komme auf 35
Da das ja eine symetrische Figur mit 5 Ecken/Achsen ist, muss das Ergebnis durch 5 teilbar sein.
Mal gucken, vielleicht finde ich ja noch mal 5 andere Dreiecke ... 
Gabi
... das scheint ja "ein Fass ohne Boden zu sein".
Ups! Sorry, meine Antwort ist weiter oben gelandet, anstatt hier unten, wo die jetztige Antwort steht (stehen sollte)!
Jedenfalls habe ich dir einen Link gegeben, wo die Antwort drin steht. Mußt nur ein wenig runter scrollen, auf der angegebenen Seite!
Konnte diese Figur jetzt nicht finden???? Kannst du einen Screenshot machen? LG Pem
Also ich komme auch auf 25. Und irgendwas innerhalb dieser 5er Schritte muß auch richtig sein. Schließlich ist es ein gleichmäßiges Fünfeck, in dem die Querverbindungen auch alle gleich sind. Deshalb gibt es von allen Dreiecksarten immer mindestens 5. Versucht doch mal, die verschiedenen Dreiechsarten mit verschiedenen Farben nachzuziehen. Dann habt ihr bald ein genaues Ergebnis. lg JaMe
du musst von den Ecken aus gehen und schauen wieviel möglichkeiten es da gibt ein Dreieck zu bilden. Sind 8 Varianten Das ganze mal 5....da 5 Ecken..ich komme auf 40 möglichkeiten. lg reni...
...denn dann hast du manche Dreiecke doppelt gewertet Ich komme auf 35 (10x1, 10x2, 10x3, 5x5) LG Stöppel
stimmt, die kleinen im Eck hab ich dann jeweils doppelt...... dann müssen die je Eck weg..dann wären es 35. Hmmm aber irgendwie stimmt das nicht... mein Mann hat die Außenlinie als grundfläche genommen..kurz überlegt und ist auf 40 gekommen.....der kann sowas normalerweise echt gut.... Wo fehlen die 5????? Lg reni
10 Einer außenrum 10 Zweier außenrum, immer zwei Nachbarteile 5 Fünfer bestehend aus dem Dreieck mit der Außenkante als Basis bis zur Gegenüberliegenden äußeren Spitze (bestehnd aus 5 Puzzleteilen) 10 Dreier: 5 mit der Spitze außen und drei Dreiecken nebeneinander und weitere 5 die von einer außen gelegenen Spitze bis zur übernächsten Spitze und dann zu einem Punkt des innen gelegenen Fünfecks gehen. 35 Welche fehlen mir?
Sorry, ich bin nicht der Paint-Profi
Figur 1 + 2 (von links nach rechts) gibt es jeweils 5x, Figur 3 10x (gespiegelt), Figur 4 nur 3x, 5 + 6 je wieder 5x
Sind aber sicher noch nicht alle ...
LG Samsine
o.T.
Hab mir mal die Mühe gemacht, das bildlich darzustellen - und habe gemerkt, dass ich mich wohl doch verzählt habe.
Laut Bild sind es 35 Dreiecke (jede Form gibt es 5 mal)
Das leere Fünfeck ist für weitere Ideen . Vielleicht gibt es ja doch mehr (und meine erstgenannten 40 stimmen doch).
Gabi
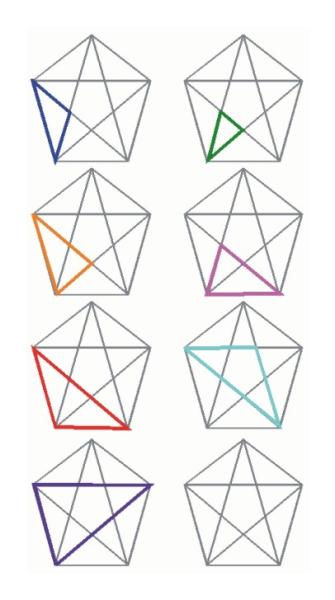
Mir fehlen zwei 3er und ich finde sie nicht *heul*
Hallo zusammen,
ich habe doch bereits in meiner ersten Antwort, die weit oben, unter den vielen anderen steht, die aber vor mir geantwortet haben, einen Link des Lösungswegs, reingestellt.
Antwort lautet: 27 Dreiecke
Schaut auf den Link von mir!
Ähm, ich finde bei dem Link zwar einen Haufen Dreiecksaufgaben, aber die hier, finde ich nicht. 27 ist schon allein deshalb nicht möglich, weil die Ausgangsfigur ein regelmäßiges Fünfeck ist und die gesamte Figur punktsymmetrisch. Das Ergebnis muss durch 5 Teilbar sein (nachdem die Mittelfigur kein Dreieck ist). Ich komme auch auf 35, wie GabiK es gezeigt hat. LG Inge
Gucke auf mein Bild oder auch auf die Erläuterung von Samsine (die Bilder gleichen meinen)
http://home.arcor.de/jamespond2/dreiecksraetsel.html und google spukt mehrere Seiten mit dieser Lösung aus... es sind 35 Dreiecke
Wenn die Ausgangsfigur ein Dreieck gewesen wäre, hättest du recht gehabt. Allerdings ist es in diesem Fall ein Fünfeck und das gibt es in dem Link nicht, im Gegensatz zum Dreieck, dass du gefunden hast. Immer erst genau hinsehen, bevor man wild drauf los rechnet oder die vermeintliche Antwort hinschreibt. Das hat mir mein Papa in jahrelanger Mathenachhilfe immer und immer wieder eingetrichtert.
Übrigens, mittlerweile bin ich bei der Antwort 35, im Gegensatz zu gestern, wo ich nur 25 gefunden habe. Aber wie richtig das nun wieder ist, mag der Himmel wissen. 