hat jemand lust auf mathematik?

Ich hatte das lange, 90, 58, 90... Hätt ich gern wieder ;)

91-59-89 ( vor Ewigkeiten ;-))

Ok, gefragt ist das Volumen des ganzen Körpers und die Oberfläche. Ich hab da schon so viel formeln zusammen, das ich vermute dass ich falsch liege ;-)

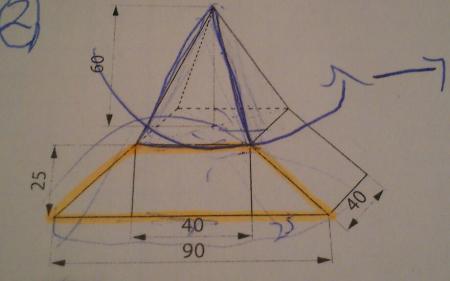
Auf die Schnelle (ich hoff, ich hab mir die Zahlen richtig notiert, zum Rechnen hab ich grad keine Lust) Körper: V1= Trapezprisma = (40+90)/2 x 25 x 40 V2 = Pyramide = 40x40x60/3 Oberfläche: 2 Trapezseiten + Rechteck unten + Rechtecke seitlich (dazu muss man noch die Länge der "Schräge" übern Pythagoras berechnen: Schräge hoch 2 = 25x25 + 25x25) Pyramide = 4 Dreiecke mit Grundseite 60 und ebenfalls noch mit Pythagoras zu berechnender Höhe Höhe Dreieck hoch 2 = 60x60+20x20

trapezprisma? ich bin beeindruckt

war natürlich das Volumen..... Oberfläche ist mir zu kompliziert..da hab ich jetzt keinen nerv .. Lg reni

Soll natürlich heissen Prisma dabei NICHT 2 mal rechnen... (ist ja zum rechteck zusammen gerechnet)

die gesamte obrerfläche setzt sich zusammen aus 2mal das rechteck, 4mal die dreiecke, 2mal die schrägen und die mantelfläche der pyramide. fläche rechteck = a*b = 40*25 = 1.000; mal 2 macht 2.000 fläche dreieck = 1/2 *g*h = 1/2*25*25 = 312,5 ; mal 4 macht 1.250 fläche schräge = a*b, b entspricht hier der dritten seite des dreiecks; die hab ich mit pythagoras ausgerechnet und 47 erhalten, daher a*b = 40*47 =1.886 ; mal 2 macht 3.772 für die mantelfläche der pyramide hab ich den rechten schenkel des dreiecks berechnet wenn man draufschaut, um daraus dann die höhe h des dreiecks der mantelfläche zu bekommen. dazu hab ich mit pythagoras die diagonale der grundfläche der pyramide berechnet (57) und halbiert (28,5), dadurch einen schenkel x erzeugt der vom mittelpunkt der pyramidengrundfläche von dem die pyramidenhöhe ausgeht zu dem punkt geht an dem der o.g. rechte schenkel startet. dann mit pythagoras den rechten schenkel ausrechnen, mit hilfe der pyramidenhöhe (60) und der halben Diagonale x (28,5) --> ergebnis abgerundet 66. dann weiter die höhe des dreiecks berechnen; dazu a*schenkel nach pythagoras umstellen und ausrechnen, bin auf eine dreieckshöhe von 63 gekommen. dann mantelfläche ausrechnen; 4*(1/2*g*h) = 4*1/2*40*63 = 5.040 summa summarum also 2.000 + 1.250 + 3.772 + 5.040 = 12.062 das ist mein ergebnis. bin auf das richtige gespannt!

volumen pyramide + volumen des quaders + zweimal volumen prisma, ergab bei mir 84.500 pyramide v = 1/3*grundflächepyramide*h = 1/3*(40*40)*60 = 32.000 quader v = a*b*c = 40*25*40 = 40.000 prisma v = grundflächeprisma*h, grundfläche entspricht dem dreieck von vorhin, daher 312,5*40 = 12.500

einmal prisma vergessen... also 97.000

ach so, der boden zählt ja wohl auch zur oberfläche... ich sollte die heizung aufdrehen, zu kalt zum denken hier... also noch 90*40 dazu... mein abschließender ergebnisvorschlag lautet dann also 15.664...

... hast du 25*40 eingesetzt, oder? Bei dem Dreieck sind aber beide Schenkel 25 lang (siehe Skizze, linke Seite). Dann kommst du mit Pythagoras auf ca. 35, dann gleicher Rechenweg wie bei dir, so dass ich am Ende bei 14738 für die Gesamtoberfläche lande. Beim Volumen habe ich ja das Gleiche raus wie du (97000), bin daher auch sehr gespannt.

nein, nicht 25; diese seite des dreiecks war doch garnicht gegeben, die hab ich vorher mit pythagoras ausgerechnet.

ja genau, ca. 35; ich hatte 37 raus, hab ich im ersten posting beschrieben. aber wieso bekommen wir dann unterschiedliche werte raus wenn wir das gleiche gemacht haben

Siehe Bild. Mir kamen deine Zahlen auch schon sehr bekannt vor. Sonst vielleicht Abweichungen durch Rundung der Zwischenergebnisse?

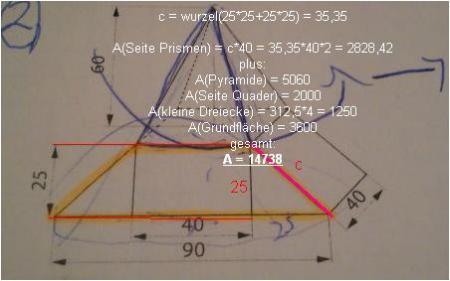
ich hab den schenkel der bei dir c heißt falsch berechnet; richtiger rechenweg, aber hab 25 und 40 zugrundegelegt statt 25 und 25.

... passend zur schon oben stehenden "Anleitung" ergibt auch V=97000 O= 14738,0712