malini
Hallo, ist hier jemand, der mir den Lösungsweg zu dieser Aufgabe kindgerecht erklären kann? Ich bin zwar nach rumprobieren draufgekommen, würde es aber dem Kind gern erklären.
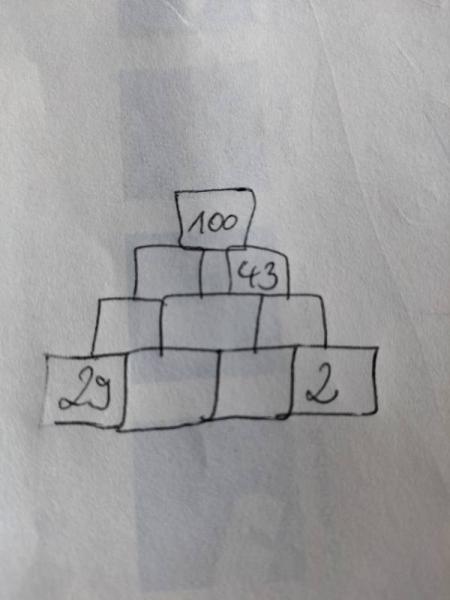
Bist du sicher, dass die so aussieht? Für mich fehlt da eine Ebene (nur 2 Steine; vorletzte Reihe), weshalb sie sich auch nicht eindeutig, also ohne Rumprobieren, lösen lässt. Bei Rechenmauern ergeben ja immer die unteren beiden den Stein darüber. Hier muss aber plötzlich die Summe aus 3 Steinen gebildet werden. Das kommt mir nicht richtig vor.
Ich habe es schlecht gezeichnet. Die zweite Reihe sind nur 2 Steine. Es sind unten 4, dann drei, dann zwei und zum Schluss der oberste.
Für mein Dafürhalten fehlt da definitiv irgendwo eine Zahl. Reihe 2 ist ja klar:100-43=57 Dann hat man Reihe 2 fertig, aber um weiter zu rechnen braucht man ja noch eine Zahl in der Reihe darunter würde ich meinen.
Ja, wir auch. Mit einer Zahl in der dritten Reihe kommt das Kind auch super zurecht mit den Mauern. Aber dadurch, dass da alle Zahlen fehlen, hat es nur mit viel ausprobieren funktioniert.
Hallo, jeweils zwei Steine nebeneinander ergeben das, was über beiden steht. In Deinem Beispiel also x+43=100 oder 100-43=x, x ist also 57. So arbeitest Du Dich die Pyramide bergab, mit der Schwierigkeit, dass eine Zahl "in der Mitte" jetzt zu mehreren Zahlen passen muss. Verständlich? Viele Grüße
Ja, an sich ist es mir klar. Wir kommen nur nicht "einfach" auf den Lösungsweg,dass ich es meinem Kind gut erklären kann. Hab selbst nur rumprobiert, relativ lang...
Hi Malini, ich würde ich es so erklären: 1. Du ziehst die Zahlen aus der untersten Reihe von der Zahl an der Spitze ab (100-29-2=69) 2. Diese Zahl teilst du durch 3 (69:3=23). 3. Dies (23) ist die Zahl in der Mitte der zweiten Reihe von unten (die mit den drei leeren Kästen). 3. Danach kannst Du Dir alle anderen Zahlen durch Subtrahieren erschließen. Unabhängig davon: - Passen Zahlenraum und Rechenarten zum Lernstand einer zweiten Klasse? - Tust Du Deinem Kind einen Gefallen, wenn die Lehrkraft denkt, es hätte die Strategie (und darum geht es bei Rechenmauern) im Unterricht verstanden? Viele Grüße!
Mein Kind ist grundsätzlich gut in Mathe und kapiert Rechenmauern an sich gut. Es geht mir nur darum, ihm zu erklären, wie es solche Mauern lösen kann. Dein Ansatz ist prima, das werde ich gleich Mal so weitergeben.
Na normalerweise beginnt man die Mauer, wo 2 Zahlen schon mal da sind und dann geht's weiter.... Das geht hier allerdings ja nur mit Probieren und find ich für ne 2. Klasse schon schwer ( ist ja für manche Eltern wahrscheinlich schon nicht leicht lösbar).
Klassische Rechenmauern sind auch wie gesagt überhaupt kein Problem. Aber wir haben es nochmal bei anderen Mauern probiert: der Tipp zur Lösung funktioniert bei allen anderen auch. Wir hatten zwar nie das Problem, dass die Division 69:3 für einen Zweitklässler eigentlich auch nicht ideal ist. Bin auf die Lösung der Lehrerin morgen gespannt. Die Aufgabe war übrigens im Arbeitsheft der 2. Klasse, von daher wird es schon eine passende Lösung geben 
.
Es gibt nur eine Lösung.
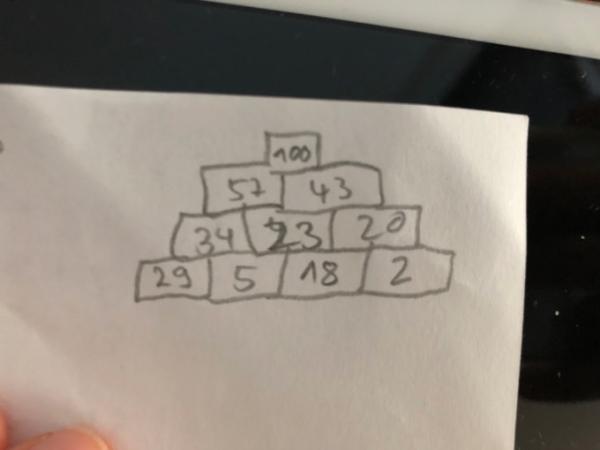
1. Variablen für die freien Steine einsetzen (s. Foto). 2. Gleichungen aufstellen. 3. Nach e auflösen.
Also: c=e+2 b=43-c Einsetzen: b=43-(e+2) =41-e d=b-e Einsetzen: d=41-2e a=29+d Einsetzen: a=29+41-2e a=70-2e a=57-b a=70-2e b=41-e Einsetzen: 70-2e=57-(41-e) 70-2e=16+e. I-70-e -3e=-54 Ix(-3) e=18 Mit e=18 kann man den Rest auflösen.
Ist vielleicht etwas über dem Niveau der 2. Klasse. Aber meine Schulzeit ist auch schon ein paar Jahre her.
Finde ich auch schwer für die 2. Klasse. Ich würde da mit einem Gleichungssystem rangehen, aber das können Zweiklässler natürlich noch lange nicht.
Finde ich auch schwer für die 2. Klasse. Ich würde da mit einem Gleichungssystem rangehen, aber das können Zweiklässler natürlich noch lange nicht.
